頭脳クイズ: 2007年10月アーカイブ
マクドナルドで「スマイルください」って言うことと「朝ミックください」って言うこと、どちらの方が恥ずかしいのだろうって真剣に考えた関東地方台風の午後でございます。
どちらも別に恥ずかしくないんじゃないかと思ったことは内緒です。
時々、ハンバーガーを無性に食べたくなるときがあります。
そんなとき、手にしたハンバーガーを見つめながら
「宇宙のどこかにはものすごーく大きい人たちがいて、その人にとっては地球がハンバーガーぐらいの大きさに見えているのかもしれない」
なんて考えるわけです。
ということで、地球の大きさに関する「青春Bブログ名物頭脳クイズ」行きましょう~。
第七問! QQQのQ~!!
question:
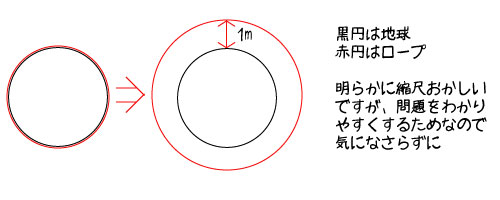
今、地球を平面としてとらえます。
地球の直径と同じサイズの円があると考えてもよいです。
その円をぐるっと回るようにロープをかけます。
ロープの長さは現在、円周と同じです。
さて、このロープの長さを今より何m伸ばせば、地球サイズのこの円から1メートル離れた円を描くことができるでしょうか。
半径や円周はすでに求められているものとします。
answer:
以下、白文字にて解答を書いています。
解答を知りたい方はマウスで選択して文字色を反転させてください。
地球の半径や円周を必要とせずに解くことができます。
地球の半径をrメートルとします
地球よりも1m外側を回るロープの半径は(r+1)メートルとなります。
地球の円周は2πrメートルです。
よって、地球よりも1m外側を回るロープの円周は2π(r+1)メートルです。
2π(r+1)=2πr+2π≒2πr+6.28
よって、元のロープよりも約6.28メートル長くすれば、地球の1メートル外側を回る円とすることができます。
また、式を見てわかるように、この答えは元々の円の大きさには左右されません。
ハンバーガーだろうと地球だろうと、同じ答えが出てきます。
地球という大きなもの故に、ものすごい長さをイメージしてしまう方がけっこう多いかなと思います。
そんなイメージを利用した頭脳クイズでございます。
わたしも最初、このクイズを見たとき、かなりの長さを想像しました。
だから答えを知ったとき、すごく驚きました。
自分の知識や推測はまだまだ不確かなものだなって実感したんです。
クリプトン | VOCALOID2特集
クリプトン・フューチャー・メディア(株)ホームページ
Wikipedia 初音ミク
藤田咲の電子庭園☆~さっきぃのおはなばたけ~
KEI画廊 - ケイガロウ
日本マクドナルド
さて、あなたが今、自分の家に帰ってきたところだとします。
鞄から鍵を取り出します。
その鍵をドアに差し込んで、回します。
さて、ドアを引きましたが、開きません。
どうしてでしょうか?
ここで思いつく答えは
1.間違った鍵を差している
2.元々鍵がかかっていなかった。つまり、鍵を開けたつもりがかけてしまっていた。
3.実はドアは押して開けるタイプであった。
4.引くときにノブを回していなかった。
5.ドアを引き開けるだけの筋力がなかった。
6.それは実は防犯対策のための開くことのないダミーのドアで本物のドアが別にある。
等々、答えはたくさん思い浮かびます。
そう、ドアはクイズの宝庫なのです。
さらに言うならば、開けるという行為がクイズの宝庫なのです。
ということで本日も青春Bのblog名物、頭脳クイズです。
第六問! QQQのQ~!!
question:
友人があなたの目の前に三つの箱を置きました。
その箱のうちの一つには宝石が入っています。残りの二つは空です。
どの箱に宝石が入っているか、友人はわかっています。あなたはわかっていません。
友人はあなたに「正解の箱を当てたら中の宝石をあげるよ」そう言いました。
箱は外見上まったく変わらないです。持って重さを確かめることはできません。
あなたは適当に一つの箱を指差しました。
すると友人は、残りの二つのうちの一つの箱を開けます。その箱は空です。友人は意図的に空の箱を開けたのです。
残った箱はあなたが選んだ一つと、あなたが選ばなかった一つの合計二つです。
すると、友人は「本当にその箱でいいかい。変えてもよいよ」そう言いました。
さて、あなたは宝石を手に入れるため、箱を変えるべきでしょうか。それとも、今選んでいる箱のままでよいでしょうか。
answer:
以下、白文字にて解答を書いています。
解答を知りたい方はマウスで選択して文字色を反転させてください。
正解は、箱を変えた方が宝石を手に入れる可能性は上がります。
理屈としては以下の通りです。
あなたが最初、三つの箱の一つを選んだとき、宝石が入っている可能性は1/3です。残り二つの箱に入っている可能性は2/3です。
しかし、友人が残りの二つの箱のうちの一つの空の箱を開けた時点で、もう一つの残った箱に宝石が入っている確率が2/3となります。
友人が空の箱の一つを開けた時点で、残りの二つの箱に宝石が入っている確率は1/2ずつだと考える方がいるかもしれません。
でも、それはありません。
なぜなら、最初に選んだ時点で1/3の確率だったわけです。
友人が箱を一つ開けたからといって確率が変わるというのはおかしいです。
だって、宝石を入れ替えたわけでもなんでもなく、ただ箱を開けただけなんですから。
話をわかりやすくするため、箱が1000個の場合を考えてみましょう。数が増えた方が直感的にわかりやすいかもしれないので。
あなたが一つの箱を選んだとき、その箱に宝石が入っている可能性は1/1000です。つまり、残りの999個の箱に宝石が入っている確率は999/1000となります。
ここで、友人が残りの999個の箱のうちの空の998個を開けたとします。
もともと、残りの999個の箱のどれかに宝石が入っている確率が999/1000なわけで、そのうちの空の998個を友人が開けた時点で、開けなかった一つの箱に宝石が入っている確率が999/1000となります。
これはとても有名なモンティ・ホールのジレンマという話です。
小沢健二さんの流星ビバップは本当に超名曲です。
Wikipedia 小沢健二
Ecology of Everyday Life : Kenji Ozawa
Wikipedia モンティ・ホール問題
ウサギとカメの話、ほとんどの人が知っているでしょう。
ウサギが油断して眠っている間に、着々と進み続けたのろまなカメが勝つという話です。
この話からわたしが学んだことは以下の三つ
・低い能力の者でも、一生懸命努力すれば高い能力のものに勝てる
・高い能力の者でも、努力を怠ると低い能力の者に負ける
・低い能力の者は努力をした高い能力の者には勝てないかもしれない。でも、それでもやっぱり、たとえ勝てないとしても努力するしか道はない。
つまり、欲しいものがあれば努力しろってことですね。
努力したからって勝てるとは限らないけれど、努力しなければ勝ちは遠ざかる一方です。
ということで、頭を柔らかくして欲しいものを手に入れようという趣旨で更新中の「頭脳クイズ」コーナーでございます。
本日はウサギとカメについてのクイズです。
有名な「アキレスとカメのパラドックス」というものをちょっと変えた問題ですね。
第五問! QQQのQ~!!
question:
ウサギとカメの物語で、ウサギは眠っていたばかりにカメに負けてしまったのです。
悔しいウサギはカメにリベンジを挑みます。
ただし、普通に勝っても悔しさが晴れないから、カメにハンデを与えることとしました。
カメはウサギよりも100m先からスタートします。
ここで、カメは一秒間に5m、ウサギは一秒間に10m進むとします。
レースが始まります。
ウサギが100m地点に到達するとき、つまりスタートから10秒後、カメは150m地点にいます。
ウサギが150m地点に到達したとき、カメは175m地点にいます。
ウサギが175m地点に到達したとき、カメは187.5m地点にいます。
ウサギが187.5m地点に到達したとき、193.75m地点にいます。
のんびりではあるものの、ウサギが進んでいる間にカメも進むわけです。
ウサギが「カメが前にいた地点」に到達したとき、カメはそれよりも前に進んでいます。
では、ウサギは永遠にカメを追い越せないのでしょうか。
answer:
以下、白文字にて解答を書いています。
解答を知りたい方はマウスで選択して文字色を反転させてください。
この後も「カメが前にいた場所にウサギが到達したとき、カメはどこまで進んでいるか」の計算を続けてみると、200mにその値が収束していくことがわかります。
つまり、この計算を繰り返しても200m以降に到達はしません。
ちなみに、200m地点(20秒後)というのは以下の数式で導き出される値であり、ウサギがカメに追いつくポイントです。
ウサギがカメに追いつく秒数をxとすると
10x = 5x + 100
x=20秒(200m地点)
もう一つ、数値を変えて例を示してみましょう。
ウサギの速度が毎秒10m、カメの速度が毎秒1m、両者の距離が最初10mだとします。
ここで、ウサギがカメに追いつくのが何秒後かを解答を求めるために方程式を立ててみましょう。
ウサギがカメに追いつく秒数をxとすると
10x = x + 10
x=10/9
x=1.111111……(循環小数)
となります。
ウサギが10m地点についたときにはカメは11m地点にいます。この時点で1秒が経過しています。
ウサギが11m地点についたときにはカメは11.1m地点にいます。この時点で1.1秒が経過しています。
ウサギが11.1m地点についたときにはカメは11.11m地点にいます。この時点で1.11秒が経過しています。
時間は1.111秒、1.1111秒、1.11111秒と進んでいきます。10/9に達することは永遠にありません。
この問題は「ウサギがカメに追いつく前」のことだけを対象として話が進められているというわけです。
兎と亀って聞くと、ハンゲームの歌謡タイピング劇場を思い出してしまう……。
Wikipedia ゼノンのパラドックス
Wikipedia ウサギとカメ
Wikipedia おぼっちゃまくん
無料ゲーム・オンラインゲームのハンゲーム - 歌謡タイピング劇場 -
今日から10月です。
10月と聞くとなんだか秋な感じがいたします。
秋といえば、芸術の秋です。
そして二番目に、クイズの秋です。
秋の夜長を頭の柔軟で過ごしてみるのも有意義なのではないでしょうか。
ということで頭脳クイズでございます。
今回もかなり有名なクイズですね。
第四問! QQQのQ~!!
question:
とあるホテルを三人の男性が訪れました。
ホテルは三人部屋の宿泊代が30000円です。三人は一人10000円ずつ支払い、宿泊しました。
その晩、ホテルの会計係が、現在割り引き期間で宿泊料が25000円だということに気づきました。
つまり、5000円多く受け取っていたわけです。
会計係はボーイに5000円を渡し、これを三人部屋の宿泊客に返すようにと指示しました。
しかし、そのボーイは5000円のうちの2000円を自らの財布に入れ、残った3000円を三人の宿泊客に返したのです。
さて、ここで疑問が起こります。
三人はそれぞれ10000円を支払い1000円を返してもらったので、一人9000円ずつの27000円支払ったことになります。
ボーイが盗んだ金額は2000円です。
27000円と2000円を足しても29000円で30000円にはなりません。
残りの1000円はどこにいってしまったのでしょうか。
answer:
以下、白文字にて解答を書いています。
解答を知りたい方はマウスで選択して文字色を反転させてください。
三人が支払った金額である27000円と、ボーイが盗んだ金額である2000円を足すことには計算上の意味がまったくありません。
だって
三人が最初に支払った金額30000円=三人が支払った金額27000円+ボーイが手にした金額2000円
って、意味不明な数式ですよね。
こう考えてみてください。
コンビニのレジで30000円払って、返ってくるお釣りが5000円のはずが、レジの間違いで3000円だった。
お店の受け取った金額が27000円、三人の受け取った金額が3000円、ちゃんと合計30000円になっています。
以下のように考えればなにも疑問などないということがわかります。
三人が最初に支払った金額30000円=三人が受け取った金額3000円+ボーイが盗んだ金額2000円+お店が受け取った金額25000円
もしくは
三人が支払った金額27000円=ボーイが盗んだ金額2000円+ホテルが受け取った金額25000円
もしくは
ホテルが受け取った金額25000円=三人が支払った金額27000円-ボーイが盗んだ金額2000円