学問のブログ記事

なにも疑問に思わずにいたことに対して、突然疑問を抱くことがあります。
たとえば、東京にないのにどうして東京ディズニーランドなんだろう、とか、フラッシュメモリはどうして読み取り専用じゃないのにROM(Read Only Memory)なのか、とか。
つい先日、花火を観に行きました。
キュルキュルキュルキュル、ババババババズババババ、ボンボン、プフーン
って威勢良くたくさん打ち上がっていました。
ものすごいオノマトペと共に人々を魅了していました(日本語の使い方変かな)。
オ・ノ・マ・ト・ペ
これまでの人生、オノマトペという言葉を「文字による音声の表現」の意味で迷いなく使ってきたわけなんですが、よくよく考えてみれば、オノマトペってなんでしょうか。
語呂のよさと、最後の「ペ」のかわいらしさでごまかされてきましたが(ごまかしているつもりは微塵もないでしょうが)、「擬音」についてオノマトペっていうのはやっぱりなんだか違和感があります。
そんな疑問を解決すべく、ちょっとオノマトペについて調べてみました。
調べてみてまずわかったのは、オノマトペがフランス語であるということ。
onomatopée
ですよ。
そして、本来は擬声語や擬音語(蛙を殴るときの「メメタァ」、大切な人を復活させるときの「ぴぴるぴるぴるぴぴるぴー」等)のみを示すんですね。
日本ではオノマトペというと擬態語(音がないことを示す「シーン」、メールするときの「めるめるめる」等)を含むことが多いですよね。
海外では日本のマンガを輸入する際になによりオノマトペの扱いに困るなんて話を聞いたことがあります。
日本における音表現が豊富だということなのかと思います。
擬音を効果的に使って表現力豊かな人間になりたいなと思った夏の一日です(使いすぎは禁物)。
※擬音語・擬声語と擬態語の使い分けが誤っていたら申し訳ありません。
東京ディズニーリゾート
Wikipedia Read Only Memory
Wikipedia 花火
Wikipedia 声喩
s-manga.net - ジョジョの奇妙な冒険
文芸ジャンキー・パラダイス ジョジョ・コーナー総目次
Wikipedia 撲殺天使ドクロちゃん
手塚治虫ワールド
Wikipedia 久米田康治
先日、若者文化の言葉について取り上げたので、言葉繋がりでもう一つ。
この間、中国人の知り合いの方に面白い話を聞きました。
「5201314」
これ、なんの意味かわかりますか?
中国語で読んでみると。
「うーあーりーいーさーいーすー(wu er ling yi san yi si)」
つまり、我愛你一生一世(wo ai ni yi sheng yi shi)、一生愛しますの意味なんだそうですよ。
数字語とでも言えばよいのでしょうか。
数字の発音に別の似た発音の文の意味を持たせているということです(似ていると言っていいかどうかは多少疑問)。
GO!GO!7188とポケベル全盛時代を思い出しました、なんとなく。
Wikipediaによると、ポケットベルって、NTTドコモの登録商標なんですね。
GO!GO!7188 official website[ラーフル]
Wikipedia 無線呼び出し
「KYってなんの意味か知ってる?」
そう聞かれたのはつい先日のことです。
テレビを見ない流行遅れなわたしは「これからよろしく」「香川県はよいところ」「管野よう子」とか無理やりKYに当てはまる日本語を思考するものの、答えは出ません。
実際は「空気読めない」の略だとのこと。
まあ、その言葉を知らないところでわたしの日常にはなんの支障もないわけです。
けれど、なんだか、だからってそのままだと自分が若者の心をなくしてしまったみたいで嫌じゃないですか。
だから若者言葉を色々と調べてみました。
そういう行為に走る時点で若者の心を失ってしまっている気もしますが……。
ということで、学習成果のごくごく一部を下に書いてみました。
KY:空気(K)読めない(Y)の略
使用例「あんなKYなやつは、美味しいミニストップのソフトクリーム食べる資格ないよね」
CKY:CAN(C)空気(K)読める(Y)の略
使用例「あの子ってCKYだから、美味しいミニストップのソフトクリームおごってあげようよ」
ぱねぇ:半端ではないの意味
使用例「ぱねぇぐらい美味いよ、ミニストップのソフトクリーム」
パギャル:中途半端なギャルの意味
使用例「パギャルにミニストップのソフトクリーム食べる資格ないよね~」
とりま:とりあえず、まあの略
使用例「とりま、ミニストップのソフトクリームで気持ち落ち着けようよ」
H/K:話は(H)変わるけど(K)の略で、手紙などに使用
使用例「明日は晴れるかな? H/K ミニストップのソフトクリーム、一日何回食べますか?」
PK:パンツ(P)食い込んでる(K)の略
使用例「あの子、ミニストップのソフトクリームの食べすぎでPK」
なかなか使う機会がなさそうな単語ばかりですが、H/Kは使ってみようかなと思います。
日本語俗語辞書
Wikipedia ギャル語
MINISTOP
MINISTOP ファーストフードメニュー
Wikipedia 管野よう子
香川県
わたくしはじゃんけんが弱いです。
人生じゃんけん勝率の統計をとったことはないですが、おそらく四割や三割程度なのではないかと思います。
そのことで人生たくさん損してきたのじゃないかと悲観的になってしまうものです。
たかがじゃんけん、されどじゃんけん、じゃんけんの人生に占める比率ってかなりのものではないかと考えるのです。
だって、「もしも絶対にじゃんけんで負けない人間に生まれていたなら」そう想像してみてください。
それはとても素晴らしいことに思えませんでしょうか。
わたしはずっと、じゃんけんに弱い自分は運の悪い人間なんだなと思ってきました。
でも、ネット上のとある記事を見て、それは決して運の問題ではなく、努力が足りないゆえの自業自得なのではないかという気持ちになったのです。
GIGAZINEというサイトにて、もう一年以上前の記事ですが、じゃんけんに勝つための7つのテクニックというものが掲載されていました。
じゃんけんの奥深さを知りました。じゃんけんも一種の学問や競技なのだなと感じました。
わたしが知っているテクニックは、そのうちの一つだけでしたね。
「一回前に相手が出した手に負ける手を出す」
なぜかと言うと、人間は連続で同じ手を出すことを避ける傾向があります。
だから、今がグーなら、次はパーかチョキになる確率が高い。だとすると、その場合はチョキを出しておけば負けない。
じゃんけんが弱いと嘆いている方、以下のリンクの記事を見てみるとよいかもしれないです。
じゃんけんに勝つための7つのテクニック - GIGAZINE
世界選手権におけるじゃんけんの様子
ちなみにわたしは多分、今後もじゃんけんで負け続けるでしょう。
箇条書きをするのに適した油性ペン……のことではありません(ちなみにマジックインキは登録商標だって知っていましたかしら)。
囚人のジレンマ、悪魔の証明に続き、新たに知った言葉を紹介するシリーズでございます。
まずは、以下をご覧ください。

とある二人のプロ野球選手の経歴を箇条書きしたものです。
まあ、名前を伏せても大抵の方は誰を示しているかわかる気がしますが。
プロ野球についての知識を持っていない方は、この二人が非常に似ているような印象を持つかもしれません。
高校野球のスターからプロ野球のスターへと進み、野球へのこだわりを持って現在も舞台を求めて戦い続ける二人……。
某プロ野球選手Aは「桑田真澄」選手、某プロ野球選手Bは「清原和博」選手です。
桑田選手と清原選手を知っている方は「二人が似ている」って印象を持ってはいないでしょう、きっと。
それでも、共通点だけを並べるとまるで二人が似ているような気分になる。
ちょっと例がわかりづらかったかもしれないですが、これを箇条書きマジックと呼びます。
類似点だけ並べると、あたかもその二つが非常に似ているような思い込みをしてしまう。
逆に言えば、箇条書きを使えば相手を情報操作しやすいとも言えます(そんなにうまくいかないでしょうが)。
過去の人とのコミュニケーションを思い出したとき、箇条書きマジックに惑わされたことも箇条書きマジックで惑わしたこともあるように思います。
Wikipediaの箇条書きマジックのページを見ていたとき、これと似た例として、DHMOが挙げられていました。
DHMOがなにか気になりますか。
Dihydrogen Monoxideの略です。とある物質です。
Wikipediaより抜粋しますと「DHMOは依存症を発症させやすい。発症すると毎日少なくとも2リットルは摂取しなければならなくなる。代表的な禁断症状として、猛烈な喉の渇きを訴える例が多く、さらに進むと幻覚を見るようになる。放置すると遅かれ早かれ死亡する。その確率は100%である。」というものです。
詳しく知りたい方は以下のリンクより「Wikipedia DHMO」をご参照ください。
言葉の力って本当にすごいですね。
「メディアが嘘を伝えるのをやめることは真実を伝えることと等しくない」という言葉も同じ類を示していますね。
抜粋や強調をした時点で真実から離れてしまう。
気をつけます、色々と。
Wikipedia 箇条書きマジック
桑田真澄 Official Web Site
オリックス・バッファローズ選手紹介 清原和博
Wikipedia マジックインキ

世の中には不思議なことがたくさんあります。
それは決して遠く大きい不思議の話ではなくて、とても身近なところでの話です。
たとえば、どうしてさお竹屋は潰れないのか(金物屋兼業だから)。
たとえば、どうしてこれまでに一つの消しゴムを使い切った記憶が残っていないのか(実際使い切っていないから)。
たとえば、どうしてつい先日掃除したばかりの部屋がひどく汚れているのか(ただの不衛生)。
たとえば、どうしてつい先日切ったばかりの爪がすごく伸びているのか(ただの不摂生)。
たとえば、どうして傘を忘れたときにだけ雨が降るのか(ただのマーフィーの法則)。
等など、不思議なことだらけの世の中です。
そして、最も代表的な不思議として、どうしてコード類は自ら意思を持っているとしか思えない不可解な絡まり方をするのか(上記写真のような)。
MP3プレイヤーのイヤホンなんかは鞄の中とかシャツのポケットとかに押し込むことがあるからまだ納得なのですが、納得できないのは電話のコードですね。
ずっと同じ場所に置いているのに、ぐるぐるぐるぐる絡まっていきます。
その理由について説明した記事がITmediaに掲載されていました。
簡単に言うと「持ち替えの際に受話器が回転するから」という理由です。
なるほどねという感じです。
もしも詳しく知りたい方は、以下のリンクをクリックくださいませ。
最後は商品宣伝になっていますが、それまでは普通にコードがねじれる現象を説明してくれています。
ITmedia Biz.ID:電話機の「コードねじねじ現象」が発生する理由
電話のコードのねじれ具合って、その人の電話の使用量の尺度になるかもしれないですね。
もしくは落ち着きのなさの尺度とかでしょうか。
先日、新たに知った言葉として「囚人のジレンマ」を紹介しました。
もう一つ同時期に知った言葉として「悪魔の証明」があります。
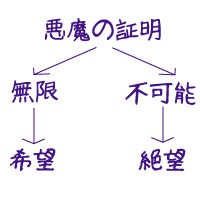
ある事象が存在することの証明は実例を一つ示した時点で終わる。
しかし、ある事象が存在しないことの証明は、存在することの証明に比べて非常に困難である場合が多い。
悪魔の証明とはそのような「存在しないことの難しさ」を示す比喩です。
たとえば、「日本に蛇がいる」ことを証明しなさいと言われたなら、日本で蛇を捕まえれば証明されます。
では「世界に一角獣がいない」ことを完全に証明できるでしょうか。それを完全に証明する術が思いつく人なんていないんじゃないでしょうか。
悪魔の証明とはこのような事例を指します。
悪魔の証明って、コミュニケーションの中で容易に持ち出してよいものではないですよね。
だって、非常に詭弁に陥りやいように思えます(否定できないということを肯定できるということに結び付けてしまいそうだという意味です)。
それが議論の場であれば議論の発展を阻止するようにも思えます。
悪魔の証明を受け入れてしまうとそこから先には進めないわけです。
もしくは、無意味に惰性的に進んでしまう。
わたくしも悪魔の証明に頼っている節があるのではないかという気がしました。
人と話しているとき、半ば屁理屈気味に悪魔の証明を持ち出しているのではないかって。
もしくは、内面において、良くも悪くも日々どこかに悪魔の証明がある気がします。
ないという証明をすることがとても困難であるという事実は、ある種、無限を意味します。
諦める理由がないことであり、それは希望が潰えないこととイコールなのではないか。
同時に、ないという証明をすることがとても困難であるという事実は、ある意味では不可能を意味します。
諦める理由を見つけられないということであり、納得する理由を見つけられないということであり、それは絶望がつきまとうこととイコールなのではないか。
色々と考えさせられた言葉です。
新しい知識を得たときの興奮というのは、本当に大きなものです。
大人になると、まるで世界の大半を知ってしまったかのようなつもりに気づかぬうちにをなってしまいます。
けれど、実際には「常識」と呼ばれるものの中の1%ですら自分は知らないように思います。
当たり前をすべて当たり前に知っている人間って、とても格好良いです。
ということで、最近わたしが知った言葉の一つを紹介いたします。
それは「囚人のジレンマ」という言葉です。ゲーム理論や経済学という分野にて使用されているそうです。
「相手が存在する事象において最適解を見つけることの難しさ」を示したモデルケースであるとでも言えばよいでしょうか。
わたしはこの話を知ったとき、非常によくできていると感動いたしました。
無知だからこそ手にした感動……無知な自分に乾杯です(乾杯している場合ではないかもしれないですが)。
囚人のジレンマとはどういうものかといいますと……。
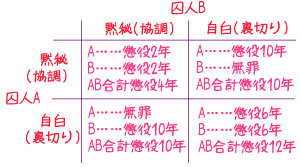
ある二人の人間が罪を犯して逮捕されたとします。二人は別々の場所にて取調べを受けることになりました。
犯行について供述しようとしない二人に対して、ある司法取引が持ちかけられるのです。
「このまま二人とも黙秘を続けた場合、二人はそれぞれ懲役二年を科されることになる。しかし、Bが黙秘を続けAが自白したならば、Aは無罪とし、Bは懲役十年とする。逆の場合も同じである。ただし、二人が自白した場合、二人に懲役六年をそれぞれ科す」
A、B共に相手の状況を知ることはできません。隔離されています。
その状況において、それぞれが最もベストな選択肢を考えるのです。
Aはあることに気づきます。
「Bが黙秘したと仮定したとき、自分は黙秘なら懲役二年、自白をしたなら無罪になる」
「Bが自白した場合、自分は黙秘なら懲役十年、自白をしたなら懲役六年となる」
「つまり、Bが黙秘を続けたとしても自白したとしても、自分は自白をした方が得になる」
Aは自白することがベストだという結論を導きます。
しかし、当然Bも同じことを考えているはずです。
二人が揃って自白をした場合、それぞれに懲役六年、合計懲役十二年となります。
最適な道を選んだはずなのに、合計で見ると最悪な結果となってしまっているのです。
このようなケースを囚人のジレンマと呼びます。
最適な解を選んだはずが、結果はうまくいっていない。
自分の得を選んだが故に損をしてしまったということになります。
相手を信じて互いに黙秘していれば懲役二年で済んだわけです。
けれど、相手は自分を裏切るかもしれないと考えると、かなりのプレッシャーで悩むでしょう。
現実社会にこのような問題が「囚人」というケースで発生するかというと、司法取引の可不可等の話等含めほとんどないかもしれません。
でも、それ以外の日常だったり商売だったりのケースにおいて、こんな「相手がいるからこそ決断が難しい」って場面はかなりあるように思います。
つい先日、とてもドキドキすることがありました。
寿司チェーン店でパックのお寿司を買って帰ったんです。
で、いざ食べようと思うと醤油がついていない!
我が家には醤油がないのです。
醤油をかけない方が身体にはよいかもしれないですが、味的にはやっぱりちょっと……。
どうしたものかとかなりドキドキいたしました。
でも、こんな事態のためにと前にとっておいた使いきりの醤油を発見し、一安心いたしました(前、二つ醤油をもらったときに一つ使わなかったのです)。
過去の自分の念入りさに乾杯です(しょうゆが入っていることを確認しなかった自分と普通に醤油を常備していない自分のことは忘れます)。
ただ、いつから置いてある使いきり醤油かわからないので(普通に電気コンロの横に投げ置いてありました)、食べているときに別のドキドキ感がありましたが……。
なんて出来事があったわけですが、もしもわたしが光の速さで移動できる人間だとしたら、即座にお寿司屋にしょうゆを貰いに行けたわけです。
お寿司の鮮度が落ちるよりも早く。
ということで最近、相対性理論がわたしのマイブームです。
「なにをいまさら」ってアインシュタインさんに叱られてしまいそうですね。
説明の必要なんてないかもしれないですが、相対性理論は特殊相対性理論と一般相対性理論の二つがあります。
それぞれの超簡単な内容は以下の通りです。
※専門知識を持っているわけではないため、本記事の正当性についての責任追及はおやめください
・特殊相対性理論
重力のない慣性系(慣性の法則が成立する座標系のこと)においては光の速度のみが一定であり、その他は時間も空間も一定ではない。
・一般相対性理論
特殊相対性理論を慣性系のみではなく一般系まで広げたもの。
今は相対性理論に至るまでの物理学の歴史についてを本で読んでいます。
相対性理論の一つのキーワードに「光」があるわけですが、その光速を求めるための様々な実験についてですね。
昔は光の速度が無限か有限かという議論もなされていたそうですね。
色々な物理学者や天文学者の方が光速の計測のために様々な実験をしたようです。
そのうちで最も個人的に面白いと思ったのが、イギリスのジェームズ・ブラッドリーさんが行った方法ですね。
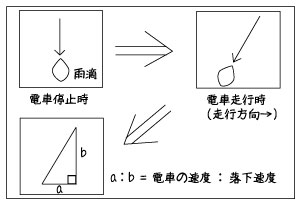
走る電車の中から雨を見ると、風がない場合、雨滴は垂直落下しているはずなのに斜めに見える。
その考えと同じで、「望遠鏡内を通る星の光」を雨滴、「地球の公転速度」を電車の速度のようにとらえて光速の測定を行えます。
電車の速度はわかっているから、後は望遠鏡を通る星の光を斜辺とした直角三角形から光速が求められるはず。
でも、ここには一つの落とし穴があります。
雨滴は頭上から落ちてくるけれど、星の光は必ずしも頭上から来ているものではないってことです。
望遠鏡から見えている星の姿は、今実際にそこにある星ではありません。
わたしたちの目から見える日の出が実際には八分前の太陽(太陽から地球に光が届くのに八分かかります)であるのと同じように、星も見えているものと実際でずれているのです。
だから光が来た方角だと思っているものが実際にはそうではないため、当然、誤差が生じてしまいます。
ブラッドリーさんのすごいところは、この事実に気づいた点です。
1700年代当時は、目に見えているものが実際にあるものだって考えが多分、常識だったでしょうから。
ブラッドリーさんはこの天体位置のずれ「光行差」を元に光速を求めたのです。
精度の問題など、求められた値は約301,000,000m/sと実際のもの(現在は299,792,458 m/sとされています)より大きい値に放てしまったものの、光速がとてつもなく高い値でありながら有限であることを証明したのです。
物理学とかの歴史って、謎を解き明かそうとする人間のロマンが詰まっていてとても面白いです。
ここまで書いてきて思ったのですが、タイトルに「相対性理論」って書いているのに「相対性理論」について語っていない。
また別の機会に……(あるかしら、別の機会)。
Wikipedia 相対性理論
Wikipedia アルベルト・アインシュタイン
Wikipedia ジェームス・ブラッドリー
Wikipedia 光速度

今日、東京地方、雨が降りましたね。
わたしは天気予報をほとんど見ない人間なので、帰り際、傘がない状態で降られました。
家まで自転車で約三十五分です。
出発時点はほとんど雨が降っていなかったので、平気だと思いました。
でも、途中からそれなりに雨が強くなり、けれど、途中で傘を買うと最初から買っておけばよかったと後悔してしまうので、途中で喫茶店には寄ったものの傘なしで帰りました。
喫茶店から出たら雨がさらに強くなっていたのは悲しかったです。
いつも雨の中で自転車を漕いでいると、とあることを考えます。
それは「速く漕ぐのと遅く漕ぐのはどちらの方が濡れないのか」というものです。
単純に考えれば、速く漕ぐ方が目的地に着くまでの時間が短いので濡れなさそうです。
雨の中にいる時間が短くなるってことですから。
でも、現実には速く漕いだ方が濡れている気がするのです。
速く漕ごうが遅く漕ごうが走行距離は変わらないです。
それを考えると自転車の速度と濡れ具合は関係ないのでしょうか。
浴びる雨の量が同じだとしたなら、短時間で濡れる分だけ気化熱で蒸発する間がなく、服の濡れ具合がひどいものになったりするのでしょうか。
自転車の速度と濡れ度合いの関係、かなり謎です。
誰か物理学的に解明した人はいないのでしょうか。