学問: 2007年10月アーカイブ
いわゆる「天才」と呼ばれている人たちについて本やネットで調べたりするのが大好きです。
そこでは常識を遥かに超えた価値観だったり才能だったりが輝いています。
スポーツの分野での「天才」より学術的分野や芸術的分野での「天才」に惹きつけられます。
それはどうしてでしょうかね。
わたしの単純な趣味嗜好によるものでしょうか。
「ずば抜けた才能」が素晴らしい方向に活かされるかどうかは別として、そのエピソードの数々に心奪われます。
そんな「天才めぐり」の日々の中で、よく目にする単語の一つとしてサヴァン症候群があります。
発育や自閉についての障害(必ずしもこれらの障害とは限らないそうですが)を持ちながらも、ある特定の分野において常識離れした能力を発揮する人たちを指す言葉です。
たとえば、有名な事例としては以下のようなものがあります(真偽の確認はしていません)。
・数千冊の本の内容をすべて暗記している
・年と日付を元に即座に曜日を答えられる。それがたとえ千年以上先の日付であっても。
・初めて聴いた曲を完全に間違えず再演奏することができる。しかも目が見えないしピアノのレッスンを受けたこともないのに。
・ものが右にあるか左にあるかの説明はできないのに複数桁の掛け算を即座に解く。
これらの能力の良し悪しについて語るつもりはありません。
ただ、こういう特殊な能力を持っている方々の思考には非常に強い興味があります。
思考ではなく価値観と置き換えてもよいかもしれない。
卓越した計算能力を持つ者には世の中の数字がどのように見えるのか。
デジカメ並の記憶力を持つ者にとって思い出とはどんなものなのか。
とあるマンガで『お互い理解しあえるのはほとんど「点」なんだよ』という印象深い台詞がありました。
身近な人と自分を比べてみても、共通する部分なんて点でしかないのかもしれない。
もしもすべての能力が同じ同士でも、視力が0.1違うだけで目に映る景色も価値観も大きく異なるのでしょう。
線として分かり合える相手なんていないのかもしれない。
人間って恐いぐらいに不思議で面白いです。
Wikipedia サヴァン症候群
Wikipedia 岩明均

子どもの頃、かの発明王エジソンの伝記を読みました。
そこに一つ、興味深いエピソードが載っていたのです。
エジソンがまだ小学生の頃のエピソードです。
先生が、子どもたちに授業をしていました。
土でつくった団子を二つ並べて、1+1が2だということを教えるのです。
それに対してエジソンは反論します。
二つの団子をくっつけてしまえば、1+1=1だという反論です(つまり、大きな一つの土団子ができるということ)。
先生はエジソンの反論を「言われたまま覚えればいいのよ」みたいな感じで拒否し、エジソンは学校を辞めて母親に勉強を習う……確かそんなエピソードでした。
子どもの頃のわたしは、エジソンは面白い発言をするなと思ったのです。
そして、1+1は2に決まっているとも思いました。エジソンをちょっと見下しました。
でも、少し冷静になってみると、エジソンが言った「1つの土団子が2つあれば大きな1つの土団子」という考えを否定できないわたしに気づくのです。
間違っているのはエジソンじゃなくて自分の方なんじゃないかと。
あれから時は流れてわたしも少し大人になって、今ではエジソンの考えに対する自分なりの解答を用意することができます。
計算式というのは単位が明確であるからこそ成り立つものだとこの口で言えるのです。
そして、単位を上手に変換すれば、1+1=1だってありえます。
つまり
小さな団子1個+小さな団子1個=小さな団子2個
という式も
小さな団子1個+小さな団子1個=大きな団子1個(※大きな団子の体積は小さな団子の二倍とする)
という式もありえるわけです。
確か単位の概念をしっかりと習うのは、小学校でも後の方だったように記憶しています(記憶違いでしたら申し訳ありません)。
それまでは確か、単位の概念を気にせず、数値のみの計算をしていました。
厳密に言えば、両辺の単位が等しい前提の計算練習ですね。
わたしは教育理論の専門家ではないですが、本当はもっと早い段階で、四則演算と同時期ぐらいに単位の概念も覚えたほうがよいのではって思うときがあります。
幼少期の思考力や理解力では無理なのかもしれないですし、他の理由があるのかもしれないですが……。
とにかく伝えたいのは、単位という概念が支えているものの大きさです。
前編と後編に分けて単位のことを書いてきて、前提の大切さ、明確なものの少なさを感じました。
だって、たとえば今回の記事で1+1=2についてさらっと流してしまいましたが、実際には1+1=2の証明って本一冊書けちゃうような難しさなんですよね。
考えすぎると頭が溶けてうにになっちゃいそうなので、これで終わりにします。
杏マナー杏マナー杏マナー杏マナー杏マナー杏マナー
杏マナー杏マナー杏マナー杏マナー杏マナー杏マナー
杏マナー杏マナー杏マナー杏マナー杏マナー杏マナー
ーナマ杏ーナマ杏ーナマ杏ーナマ杏ーナマ杏ーナマ杏
ーナマ杏ーナマ杏ーナマ杏ーナマ杏ーナマ杏ーナマ杏
ーナマ杏ーナマ杏ーナマ杏ーナマ杏ーナマ杏ーナマ杏
杏マナー杏マナー杏マナー杏マナー杏マナー杏マナー
杏マナー杏マナー杏マナー杏マナー杏マナー杏マナー
杏マナー杏マナー杏マナー杏マナー杏マナー杏マナー
一年以上前、このblogにて、人間の目の曖昧さについてちょっとだけ書きました。
上記の杏マナー、斜めになって見えますよね。
その際、残像効果を利用した下記の写真を紹介しました。
画像の上にマウスカーソルを持っていくとモノクロの写真が映るんですね。
カーソルを外すと写真ではなくイラストになります。
カーソルを外した状態で中心の黒い点を30秒ほど凝視してください。
またカーソルを乗っけると……。
あれから一年と三ヵ月、とあることがネット上で話題になっているのを見つけました。
かなり衝撃的でした。わたしの顔にくっついているこの目はわたしの目だけれど、実はわたしはわたしの目のことをほとんどわかっていないんだな~、みたいな感じです。
上記のページにて紹介されていた下記のページもかなり驚きでした。
えっ、本当に静止画なの? 最初に注意書きされていますが、車酔いしやすい方は見ない方がよいかもしれないです。
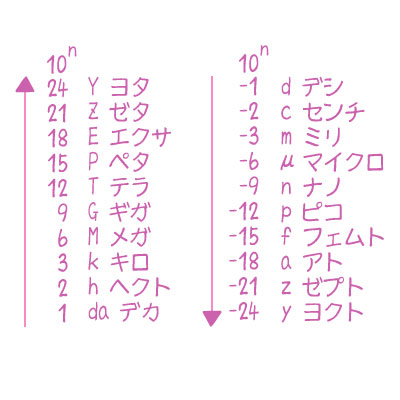
学生時代、単位の基本は国際単位系基本単位の七つであるという講義を受けたことがあります。
長さのm(メートル)、質量のkg(キログラム)、時間のs(秒)、電流のA(アンペア)、熱力学温度のK(ケルビン)、物質量のmol(モル)、光度のcd(カンデラ)の七つです。
国際単位系という名前の通り、国際的に通用する単位群です。
この七つが最初にあり、その他補助単位等が存在します。
習った内容をそのまま覚え、単位についてさらに深く学ぼうとすることなく生きてきました。
そんなわたし、この国際単位系について、恥ずかしながら最近になってとある事実を知ったのです。
正確には、その事実を知識として持ってはいたものの、なんの疑問も抱かず生きてきたというべきでしょうか。
その事実についてお話しする前に、国際単位系についてもう少し説明します。
さきほど紹介した単位の七つのうちのほとんどが普遍的な物理法則によって定義されています。
たとえば、秒については「セシウム133原子の基底状態の二つの超微細準位の間の遷移に対応する放射の周期の9192631770倍の継続時間」という定義がされています。
多くの方にとっては意味不明な定義でしょう。
でも、曖昧で変化があるような定義では、後々大問題が起こりえます。
だって、社会は単位を基準に動いているのですから。
もしも今日から1cmの長さの基準が変わったとしたらと想像してみてください。
今の1cmが明日から2cmの扱いになったとしたらって。
かなりの混乱が世界を包むだろうことが想像できるのではないでしょうか。
この国際単位系についてのわたしにとっての新事実というのが、kgだけは物理法則による定義がされていないということです。
学生時代にも聞いた話ですが、深く考えていなくて、よくよく考えてみるとびっくりな事実だなと。
キログラムは現在「国際キログラム原器の質量」と定義されています。
ちなみに国際キログラム原器というのはフランスに保管されている円柱です。プラチナとイリジウムでできています。
つまり、壊れるものです。
もしかしたら突然消失してしまうことだってありえます。
消失したらどうなるかって言いますと、世界中における重さの概念がなくなる……ってことはさすがにないか。
実際には、「そんな最悪の事態」を学者の方々も想定しているでしょうから、なるべく混乱が少ないような手を打つとは思います。
国際キログラム原器の複製品が国々に配布されているから、それを使ったりするのでしょうかね、そういう事態では?
ただ、複製品とオリジナルの重さが完全に同じだという保証があるわけではなく、というか重さは厳密には違うでしょうし……。
消えるや壊れるという事態まで行かないとしても、物質である以上、磨耗するだろうし……。
と、なんだか心配(妄想)してしまうのです。
そして、わたしなんかよりも何十倍も何メガ倍も何ヨタ倍も学者の方々が心配しているわけで、キログラムの物理法則による定義は議論中だそうです。
独立行政法人産業技術総合研究所 計量標準総合センター 国際単位系(SI)
Wikipedia 単位
Wikipedia 国際単位系