学問: 2007年5月アーカイブ
先日、新たに知った言葉として「囚人のジレンマ」を紹介しました。
もう一つ同時期に知った言葉として「悪魔の証明」があります。
ある事象が存在することの証明は実例を一つ示した時点で終わる。
しかし、ある事象が存在しないことの証明は、存在することの証明に比べて非常に困難である場合が多い。
悪魔の証明とはそのような「存在しないことの難しさ」を示す比喩です。
たとえば、「日本に蛇がいる」ことを証明しなさいと言われたなら、日本で蛇を捕まえれば証明されます。
では「世界に一角獣がいない」ことを完全に証明できるでしょうか。それを完全に証明する術が思いつく人なんていないんじゃないでしょうか。
悪魔の証明とはこのような事例を指します。
悪魔の証明って、コミュニケーションの中で容易に持ち出してよいものではないですよね。
だって、非常に詭弁に陥りやいように思えます(否定できないということを肯定できるということに結び付けてしまいそうだという意味です)。
それが議論の場であれば議論の発展を阻止するようにも思えます。
悪魔の証明を受け入れてしまうとそこから先には進めないわけです。
もしくは、無意味に惰性的に進んでしまう。
わたくしも悪魔の証明に頼っている節があるのではないかという気がしました。
人と話しているとき、半ば屁理屈気味に悪魔の証明を持ち出しているのではないかって。
もしくは、内面において、良くも悪くも日々どこかに悪魔の証明がある気がします。
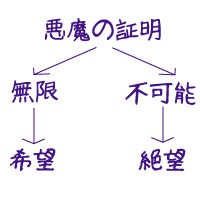
ないという証明をすることがとても困難であるという事実は、ある種、無限を意味します。
諦める理由がないことであり、それは希望が潰えないこととイコールなのではないか。
同時に、ないという証明をすることがとても困難であるという事実は、ある意味では不可能を意味します。
諦める理由を見つけられないということであり、納得する理由を見つけられないということであり、それは絶望がつきまとうこととイコールなのではないか。
色々と考えさせられた言葉です。
新しい知識を得たときの興奮というのは、本当に大きなものです。
大人になると、まるで世界の大半を知ってしまったかのようなつもりに気づかぬうちにをなってしまいます。
けれど、実際には「常識」と呼ばれるものの中の1%ですら自分は知らないように思います。
当たり前をすべて当たり前に知っている人間って、とても格好良いです。
ということで、最近わたしが知った言葉の一つを紹介いたします。
それは「囚人のジレンマ」という言葉です。ゲーム理論や経済学という分野にて使用されているそうです。
「相手が存在する事象において最適解を見つけることの難しさ」を示したモデルケースであるとでも言えばよいでしょうか。
わたしはこの話を知ったとき、非常によくできていると感動いたしました。
無知だからこそ手にした感動……無知な自分に乾杯です(乾杯している場合ではないかもしれないですが)。
囚人のジレンマとはどういうものかといいますと……。
ある二人の人間が罪を犯して逮捕されたとします。二人は別々の場所にて取調べを受けることになりました。
犯行について供述しようとしない二人に対して、ある司法取引が持ちかけられるのです。
「このまま二人とも黙秘を続けた場合、二人はそれぞれ懲役二年を科されることになる。しかし、Bが黙秘を続けAが自白したならば、Aは無罪とし、Bは懲役十年とする。逆の場合も同じである。ただし、二人が自白した場合、二人に懲役六年をそれぞれ科す」
A、B共に相手の状況を知ることはできません。隔離されています。
その状況において、それぞれが最もベストな選択肢を考えるのです。
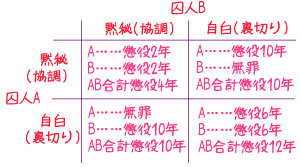
Aはあることに気づきます。
「Bが黙秘したと仮定したとき、自分は黙秘なら懲役二年、自白をしたなら無罪になる」
「Bが自白した場合、自分は黙秘なら懲役十年、自白をしたなら懲役六年となる」
「つまり、Bが黙秘を続けたとしても自白したとしても、自分は自白をした方が得になる」
Aは自白することがベストだという結論を導きます。
しかし、当然Bも同じことを考えているはずです。
二人が揃って自白をした場合、それぞれに懲役六年、合計懲役十二年となります。
最適な道を選んだはずなのに、合計で見ると最悪な結果となってしまっているのです。
このようなケースを囚人のジレンマと呼びます。
最適な解を選んだはずが、結果はうまくいっていない。
自分の得を選んだが故に損をしてしまったということになります。
相手を信じて互いに黙秘していれば懲役二年で済んだわけです。
けれど、相手は自分を裏切るかもしれないと考えると、かなりのプレッシャーで悩むでしょう。
現実社会にこのような問題が「囚人」というケースで発生するかというと、司法取引の可不可等の話等含めほとんどないかもしれません。
でも、それ以外の日常だったり商売だったりのケースにおいて、こんな「相手がいるからこそ決断が難しい」って場面はかなりあるように思います。
つい先日、とてもドキドキすることがありました。
寿司チェーン店でパックのお寿司を買って帰ったんです。
で、いざ食べようと思うと醤油がついていない!
我が家には醤油がないのです。
醤油をかけない方が身体にはよいかもしれないですが、味的にはやっぱりちょっと……。
どうしたものかとかなりドキドキいたしました。
でも、こんな事態のためにと前にとっておいた使いきりの醤油を発見し、一安心いたしました(前、二つ醤油をもらったときに一つ使わなかったのです)。
過去の自分の念入りさに乾杯です(しょうゆが入っていることを確認しなかった自分と普通に醤油を常備していない自分のことは忘れます)。
ただ、いつから置いてある使いきり醤油かわからないので(普通に電気コンロの横に投げ置いてありました)、食べているときに別のドキドキ感がありましたが……。
なんて出来事があったわけですが、もしもわたしが光の速さで移動できる人間だとしたら、即座にお寿司屋にしょうゆを貰いに行けたわけです。
お寿司の鮮度が落ちるよりも早く。
ということで最近、相対性理論がわたしのマイブームです。
「なにをいまさら」ってアインシュタインさんに叱られてしまいそうですね。
説明の必要なんてないかもしれないですが、相対性理論は特殊相対性理論と一般相対性理論の二つがあります。
それぞれの超簡単な内容は以下の通りです。
※専門知識を持っているわけではないため、本記事の正当性についての責任追及はおやめください
・特殊相対性理論
重力のない慣性系(慣性の法則が成立する座標系のこと)においては光の速度のみが一定であり、その他は時間も空間も一定ではない。
・一般相対性理論
特殊相対性理論を慣性系のみではなく一般系まで広げたもの。
今は相対性理論に至るまでの物理学の歴史についてを本で読んでいます。
相対性理論の一つのキーワードに「光」があるわけですが、その光速を求めるための様々な実験についてですね。
昔は光の速度が無限か有限かという議論もなされていたそうですね。
色々な物理学者や天文学者の方が光速の計測のために様々な実験をしたようです。
そのうちで最も個人的に面白いと思ったのが、イギリスのジェームズ・ブラッドリーさんが行った方法ですね。
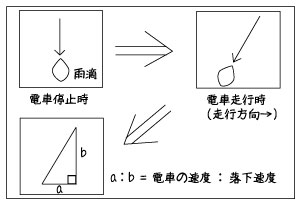
走る電車の中から雨を見ると、風がない場合、雨滴は垂直落下しているはずなのに斜めに見える。
その考えと同じで、「望遠鏡内を通る星の光」を雨滴、「地球の公転速度」を電車の速度のようにとらえて光速の測定を行えます。
電車の速度はわかっているから、後は望遠鏡を通る星の光を斜辺とした直角三角形から光速が求められるはず。
でも、ここには一つの落とし穴があります。
雨滴は頭上から落ちてくるけれど、星の光は必ずしも頭上から来ているものではないってことです。
望遠鏡から見えている星の姿は、今実際にそこにある星ではありません。
わたしたちの目から見える日の出が実際には八分前の太陽(太陽から地球に光が届くのに八分かかります)であるのと同じように、星も見えているものと実際でずれているのです。
だから光が来た方角だと思っているものが実際にはそうではないため、当然、誤差が生じてしまいます。
ブラッドリーさんのすごいところは、この事実に気づいた点です。
1700年代当時は、目に見えているものが実際にあるものだって考えが多分、常識だったでしょうから。
ブラッドリーさんはこの天体位置のずれ「光行差」を元に光速を求めたのです。
精度の問題など、求められた値は約301,000,000m/sと実際のもの(現在は299,792,458 m/sとされています)より大きい値に放てしまったものの、光速がとてつもなく高い値でありながら有限であることを証明したのです。
物理学とかの歴史って、謎を解き明かそうとする人間のロマンが詰まっていてとても面白いです。
ここまで書いてきて思ったのですが、タイトルに「相対性理論」って書いているのに「相対性理論」について語っていない。
また別の機会に……(あるかしら、別の機会)。
Wikipedia 相対性理論
Wikipedia アルベルト・アインシュタイン
Wikipedia ジェームス・ブラッドリー
Wikipedia 光速度