学問: 2006年11月アーカイブ
先日、掛け算シリーズ三部作をこのblogにて書きました。
で、完結と書きましたが、今回はその番外編です(番外編がやたら長く続いたらごめんなさい)。
職場にて線を引くだけで掛け算の話をしていたら、今回紹介する指で掛け算を教えてもらいました。
けっこう有名な方法らしいですが、わたしは初耳でした。
6×6~10×10までしかできないので、実用性には欠けるかもしれませんが、ユニークで面白かったので紹介いたします。
一応ここ、クリエイターサイトなんですけどね(笑)
あるいはこの応用版(上限を上げたもの)とかがあるのかなと期待したりしています。
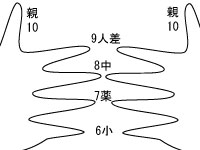
まず、両手の平を広げます。上の絵では、左側が左手、右側が右手として考えます。
そして、上の親指から順番に小指まで、10から6とします。
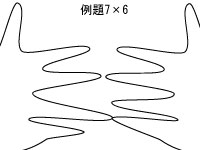
今回は例題として7×6を解いてみます。
左手の7(薬指)と右手の6(小指)をくっつけます。
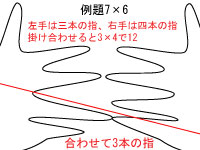
くっつけた指を境界線として考えると、くっつけた指以下に合計3本の指があります。
また、くっつけた指より上には左手が3本、右手が4本の指があります。この3と4を掛け合わせると12になります。
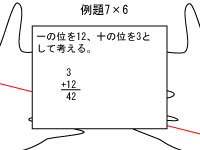
くっつけた指以下にあった本数の3を十の位、くっつけた指より上にあった指を掛け合わせた12を一の位とします。
12は10を桁上がりさせて2となり、3は下位からの桁上がりを足して4となります。
なので答えは42です。
7×6=42、正しいですよね。
最後にもう一度言っておきますが、ここはクリエイターサイトです!
以下、過去に書いた掛け算関係の三つの記事です。
高速掛け算メソッド「繰り上がり分離法」
掛け算2.0
線を引くだけで掛け算
つい先日読んだ週刊誌に、数字の裏まで読む賢い人間になれということが書かれていました。
世の中には数字で表せないことがたくさんあります。
でも、数字で表さないとどうにもならないこともたくさんあると思います。
数字を上辺だけでとらえることはきっと危険でしょう。
でも、そこから、その数字が算出されるにいたった背景や精神状況なんかまで読み解くと、多くを知ることができる気がします。
物事を数字にすることで救われることがあれば、数字にすることで傷つくこともある……。
数字の話ばかりしているけれど、数字だけが大切だというつもりはないです。
数字ではないことも大切です。
どちらも大切だからこそ、わたしはちょっと嫌われがちな数字の味方をしている……のかしら?
ということで、掛け算シリーズ第三弾、ネット上にて発見した高速掛け算メソッド「繰り上がり分離法」のお話です。
たいていの人は九九と足し算はマスターしているということに着目した方法です。
わたしはこれを知ったとき、目からうろこの感動ものでした。
いつものごとく、152×231を計算しながら説明いたします。
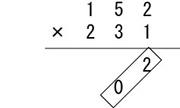
まず、普通の筆算と同じく、下一桁同士を掛けます。
ただ、普通と違うのは十の位と一の位を、斜めに書くことです。
ここでは2×1=02なので、1の左下に0を書きます。
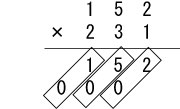
同じ要領で5×1と1×1の答えも書きます。
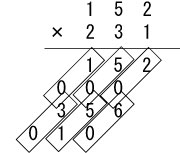
さらに続けて、152の十の位である5と231の各桁との掛け算の答えも書いていきます。
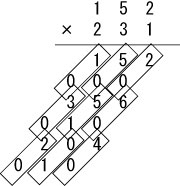
同じく152の百の位である1と231の各桁との掛け算の答えも書いていきます。
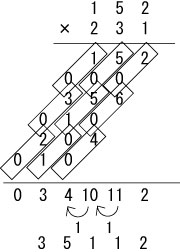
最後に計算結果を足し算して答えが出ます。
35112、正解です!
通常の筆算での桁上がりの処理を気にするのが最後の足し算だけのため、原理的には計算ミスがかなり減るものと思います。
実際には慣れの問題がありますが。
三回に亘った掛け算シリーズはこれで完結です。
誰でも知っている掛け算についての話題、シンプルだからこそ面白いとわたしは思いました。
この記事で身近なものへの好奇心が少しでも喚起され、さらにそれがクリエイティブ魂に繋がったら嬉しいわ! なんて思いました。
好奇心って、勇気や自己啓発以上の力を持つことがきっとけっこうあると思うのです。
数字が好きな人にはロマンチストが多いらしい。
それって、なんだか納得できます。
数字って、具体的な分、夢を見やすいと思うのです。
たとえば、スポーツで、現在100m走の世界記録はアサファ・パウエル選手の9秒77ですが、「9秒7を最初に切るのは世界の誰だろう」という夢を見られます。
走り幅跳びで世界記録はマイク・パウエル選手の8m95cmですが「人類初の9mジャンパーはいつ現れるだろう」と夢が見られます。
ということで(どういうことで?)、一昨日の「線を引くだけで掛け算」に続いてまた、ネット上で見つけた掛け算の手法です。
今回は前回のより実用性が高いと思います。
例として152×231を計算してみました。

まず、3桁×3桁なので、3×3の升目を書きます。
そして、左上から右下に向かって、「1」「5」「2」「2」「3」「1」の順番に記述します。
また、升目のすべての点を通るように、右上から左下への真っ直ぐな線を引きます。

次に、各升目に、欄外上部の数値と欄外右部の数値を掛け合わせた値を記述します。
値の十の位を左、一の位を右に書きます。
たとえば、左上の升目は「1×2=2」なので、「0」「2」と書いています。
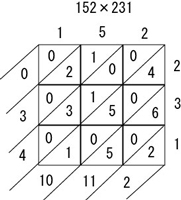
次に、升目内の値を、斜めにすべて足していきます。
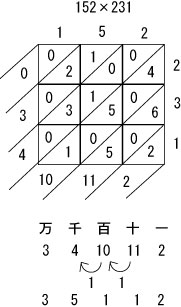
求めた数値(左と下の欄外に書かれた数字)を、左上から順番に並べます。
「3」「4」「10」「11」「2」です。
10以上のものは桁上がりさせます。
「3」「5」「1」「1」「2」になります。
152×231=35112で、正しい結果が求められました。
やはりやっていることは筆算と変わりませんが、計算ミスは減りそうに思います。
しっかりとした筆算を覚えるのがベストであるとしても、一時的に正しく計算したいときには良い方法ではと思います。
それに、こういうユニークな方法を知って、一般に敬遠されがちな「計算」という分野に対して興味を持ってもらえたら嬉しいです。
ちなみにこの掛け算話、まだ続きます。
次が完結編の予定です。
数字が好きです。
偏差値だったりなにもかもを数字化する風潮って否定的意見も多いようですが、わたしは肯定派です、多分。
わかりやすくなっているからこそ目標として明確だし、曖昧よりはずっと良いのではないかと。
数値化することで自分になにが足りないか、なにが足りているか、自分がどの位置にいるのかがわかります。
就職活動の能力についても偏差値かしようという動きがあるらしいですね。少し前にニュースで見ました。
ただ、もちろん、中途半端に一部分だけを数値化して、それですべてをわかった気になってしまう風潮もあるわけで、数字って簡単に人を欺けるわけで、そういう意味では反対派かもしれないです。
安易な数値化は反対ということかしら?
まあ、そんな話は置いておきまして、わたしはとにかく数字が好きです。
今日、ネット上で、ある掛け算の方法を知りました。
役に立つかどうかは別として、個人的にすっごい面白い計算方法だと思ったので紹介いたします!
以下、例題に画像をつけて説明いたします。
152×231を計算してみました。

まず、左上から順番に右上へと1本、5本、2本の真っ直ぐな線を引きます。
本数は計算する数値に合わせます。
今回は152だからこの本数です。

次に、231についても同じように、左下から順番に右下へと2本、3本、1本と真っ直ぐな線を引きます。
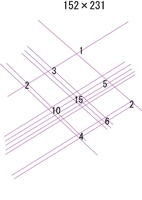
次に、各まとまりについて、交差点の数を数えます。
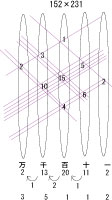
次に、左右の位置が同じ部分について、さきほど数えた交差点数を足し算します。
そして、右から順番に、一の位、十の位、百の位、千の位、万の位と考えます。
各桁10以上は桁上がりさせます。
答えが出ました!
35112、正解ですよね。
実際のところ、考え方は普通の筆算と変わらないですし、線を引く手間や交差点を数える手間があります。
ただ、数字が苦手だとこの方がわかりやすいと思いますし(数字を得意になることが本来の道だとしても、一時的な計算としては有益な方法かなと思います)、なにより、見た目的に面白いので気に入りました!
これとは違う面白い別の掛け算の方法も見つけましたので、後日紹介いたします!