高速掛け算メソッド「繰り上がり分離法」
つい先日読んだ週刊誌に、数字の裏まで読む賢い人間になれということが書かれていました。
世の中には数字で表せないことがたくさんあります。
でも、数字で表さないとどうにもならないこともたくさんあると思います。
数字を上辺だけでとらえることはきっと危険でしょう。
でも、そこから、その数字が算出されるにいたった背景や精神状況なんかまで読み解くと、多くを知ることができる気がします。
物事を数字にすることで救われることがあれば、数字にすることで傷つくこともある……。
数字の話ばかりしているけれど、数字だけが大切だというつもりはないです。
数字ではないことも大切です。
どちらも大切だからこそ、わたしはちょっと嫌われがちな数字の味方をしている……のかしら?
ということで、掛け算シリーズ第三弾、ネット上にて発見した高速掛け算メソッド「繰り上がり分離法」のお話です。
たいていの人は九九と足し算はマスターしているということに着目した方法です。
わたしはこれを知ったとき、目からうろこの感動ものでした。
いつものごとく、152×231を計算しながら説明いたします。
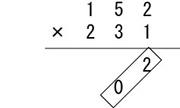
まず、普通の筆算と同じく、下一桁同士を掛けます。
ただ、普通と違うのは十の位と一の位を、斜めに書くことです。
ここでは2×1=02なので、1の左下に0を書きます。
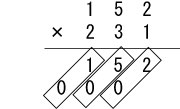
同じ要領で5×1と1×1の答えも書きます。
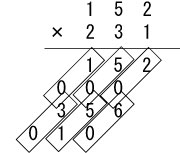
さらに続けて、152の十の位である5と231の各桁との掛け算の答えも書いていきます。
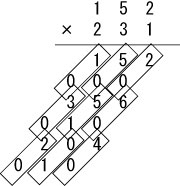
同じく152の百の位である1と231の各桁との掛け算の答えも書いていきます。
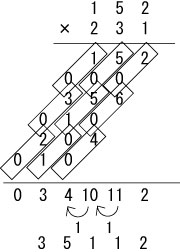
最後に計算結果を足し算して答えが出ます。
35112、正解です!
通常の筆算での桁上がりの処理を気にするのが最後の足し算だけのため、原理的には計算ミスがかなり減るものと思います。
実際には慣れの問題がありますが。
三回に亘った掛け算シリーズはこれで完結です。
誰でも知っている掛け算についての話題、シンプルだからこそ面白いとわたしは思いました。
この記事で身近なものへの好奇心が少しでも喚起され、さらにそれがクリエイティブ魂に繋がったら嬉しいわ! なんて思いました。
好奇心って、勇気や自己啓発以上の力を持つことがきっとけっこうあると思うのです。
素晴らしいトラックバックありがとうございます。2年以上前に発表したコラムですが、ときどきたまに話題に上ることがあります。今回斜め線のYoutubeがきっかけだと思いますが、繰り上がりを解決する、という意味ではまだまだ負けていないと実感しますww
//とおりすがりの業界人様
書き込みありがとうございます。実用性という点で言うならば、ここで紹介した他の二つの方法よりも上を行っていると思います。
もちろん学問とは効率の良さや楽しさだけを追い求めるものではないですが、効率や楽しさが重要なことも確かであり、その点において、この手法は感動的でした。これまで長い期間生活の中で掛け算のお世話になりながら、一度もこのような手法があることを考えもせず、学校で並んだ方法をただただ反復してきたことを実感しました。身近に未知なる可能性がまだまだあるということを教えていただき、感謝の気持ちでいっぱいです。
本当にありがとうございます。