掛け算2.0

数字が好きな人にはロマンチストが多いらしい。
それって、なんだか納得できます。
数字って、具体的な分、夢を見やすいと思うのです。
たとえば、スポーツで、現在100m走の世界記録はアサファ・パウエル選手の9秒77ですが、「9秒7を最初に切るのは世界の誰だろう」という夢を見られます。
走り幅跳びで世界記録はマイク・パウエル選手の8m95cmですが「人類初の9mジャンパーはいつ現れるだろう」と夢が見られます。

ということで（どういうことで？）、一昨日の「線を引くだけで掛け算」に続いてまた、ネット上で見つけた掛け算の手法です。
今回は前回のより実用性が高いと思います。
例として152×231を計算してみました。

まず、3桁×3桁なので、3×3の升目を書きます。
そして、左上から右下に向かって、「1」「5」「2」「2」「3」「1」の順番に記述します。
また、升目のすべての点を通るように、右上から左下への真っ直ぐな線を引きます。

次に、各升目に、欄外上部の数値と欄外右部の数値を掛け合わせた値を記述します。
値の十の位を左、一の位を右に書きます。
たとえば、左上の升目は「1×2=2」なので、「0」「2」と書いています。

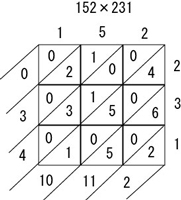
次に、升目内の値を、斜めにすべて足していきます。

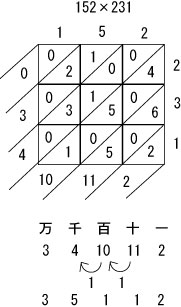
求めた数値（左と下の欄外に書かれた数字）を、左上から順番に並べます。
「３」「４」「１０」「１１」「２」です。
10以上のものは桁上がりさせます。
「３」「５」「１」「１」「２」になります。
152×231=35112で、正しい結果が求められました。

やはりやっていることは筆算と変わりませんが、計算ミスは減りそうに思います。
しっかりとした筆算を覚えるのがベストであるとしても、一時的に正しく計算したいときには良い方法ではと思います。
それに、こういうユニークな方法を知って、一般に敬遠されがちな「計算」という分野に対して興味を持ってもらえたら嬉しいです。

ちなみにこの掛け算話、まだ続きます。
次が完結編の予定です。

Wikipedia　100メートル走
Wikipedia　走り幅跳び