2006年11月アーカイブ
先日、掛け算シリーズ三部作をこのblogにて書きました。
で、完結と書きましたが、今回はその番外編です(番外編がやたら長く続いたらごめんなさい)。
職場にて線を引くだけで掛け算の話をしていたら、今回紹介する指で掛け算を教えてもらいました。
けっこう有名な方法らしいですが、わたしは初耳でした。
6×6~10×10までしかできないので、実用性には欠けるかもしれませんが、ユニークで面白かったので紹介いたします。
一応ここ、クリエイターサイトなんですけどね(笑)
あるいはこの応用版(上限を上げたもの)とかがあるのかなと期待したりしています。
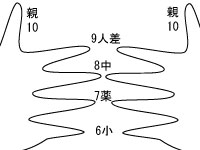
まず、両手の平を広げます。上の絵では、左側が左手、右側が右手として考えます。
そして、上の親指から順番に小指まで、10から6とします。
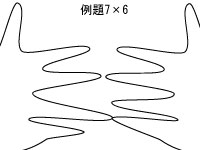
今回は例題として7×6を解いてみます。
左手の7(薬指)と右手の6(小指)をくっつけます。
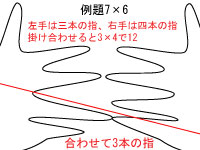
くっつけた指を境界線として考えると、くっつけた指以下に合計3本の指があります。
また、くっつけた指より上には左手が3本、右手が4本の指があります。この3と4を掛け合わせると12になります。
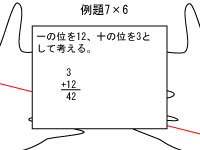
くっつけた指以下にあった本数の3を十の位、くっつけた指より上にあった指を掛け合わせた12を一の位とします。
12は10を桁上がりさせて2となり、3は下位からの桁上がりを足して4となります。
なので答えは42です。
7×6=42、正しいですよね。
最後にもう一度言っておきますが、ここはクリエイターサイトです!
以下、過去に書いた掛け算関係の三つの記事です。
高速掛け算メソッド「繰り上がり分離法」
掛け算2.0
線を引くだけで掛け算
いまさら説明の必要はないでしょうアジア最大級アートイベント「デザインフェスタ」のvol.24がついに2006年12月2日(土)3日(日)に東京ビッグサイトにて行われます。
約6000人ものクリエイターが参加し、各々の魂を表現するアーティストの祭典です。毎年二回行われています。
残念ながら青春Bとして今回のデザインフェスタには絡みませんが、トップページクリエイターリンクにてリンクさせていただいている方の何名かが参加いたします。
この場を借りて紹介させていただきたいと思います。
MARYCO(イラスト) サイト:HONEY BUNNY
ブース番号:C-470
WinterGardenと題して個展を開催します。
各日とも先着25名の方にプレゼントがあるそうです。
Satoko Chiba(イラスト) サイト:HONEY
ブース番号:A-537,538,539
チバサトコ×ingectar-e名義にて植物園をコンセプトとしたイラストでのブース展示を行います。
カレンダーやポストカードの販売も行われるそうです。
うみの(写真) サイト:日々の日柄
ブース番号:C-264
青春Bにも参加してくださっているうみのさん所属の団体root7も出展いたします。
テーマは「出荷」多種多様なクリエイターの作品を世に届けるというイメージにてブースを構築するようです。
その場にいるだけで熱くなるこのイベント、ぜひぜひ皆様足を運んでみてはいかがでしょうか。

検索キーワードチェックツールSEO(SearchEngineOle)ってご存知でしょうか?
URLとキーワードを指定すると、そのURLのサイトがそのキーワードによって各検索エンジン(google、yahoo、MSNなど)で何位に表示されるかを教えてくれるってサイトです。
SEO(Search Engine Optimization)のために非常に有効なサイトで、当サイトのリンク集3(Webクリエイター向け)にも掲載しています。
わたしも使っています。SEOのためというより、自分のサイトがとあるキーワードで何位なのかを知るのが面白いから(笑)
ということで今回はこのツールで様々なキーワードにて青春Bを検索した結果をご紹介!
すべて、Googleでの検索順位です。
キーワード:Flash素材 結果:338位
まあ、こんなものでしょうか……。素材数それほど多くないし、素材メインじゃないし……。(自己弁護)
キーワード:クリエイティブライフ 結果:23位
それなりに上位だけど、はたしてこのキーワードで検索する人がどれだけ日本にいるのかしら?
というか、本来もっと上位にいなくてはいけない!
目指せ1位!!
キーワード:青春B 結果:1位
すいません、1位が見たいのでサイトタイトル入れました。
キーワード:多口カタン 結果:1位
とりあえず稀(あるいは唯一?)な名前であることを確認。
キーワード:掛け算 結果:21位
掛け算というワードで検索する人がどれだけいるかはわかならいけれど、なんだか嬉しいです。
キーワード:謎の彼女X 結果:21位
このマンガ読んでいる人、少ないのかな……。
キーワード:うすた京介 結果:17位
blogで二度ほど日本一のギャグ漫画家として紹介していますね。
キーワード:豊島園遊園地 結果:4位
blogで取り上げましたが、ちょっと順位、上すぎやしませんか?
キーワード:エロイムエッサイム 結果:38位
水木しげるさんについて何度かとりあげましたからね。
キーワード:パブロン 結果:45位
このblogを見ても風邪は治りません。というか、悪化します。
キーワード:青酸カリ 結果:22位
このキーワードで検索して訪れてきた人の役には絶対に立てていない自信があります!
キーワード:カラメルシロップ 結果:10位
きっとお菓子好きな人がこのワードで到達するでしょう。お菓子の話題のないこのサイトに。申し訳ありません。
ちなみに「青酸カリ カラメルシロップ味」というこのblogのタイトルは、辛いことも楽しいこともある、みたいな意味です(多分)。
つまり青酸カリが辛さ、カラメルシロップが楽しさを意味しているわけです。
せめても、カラメルシロップというキーワードでたどり着いた方のために、その作り方を書いておきます。
「鍋に砂糖と水を3:1ぐらいの割合で入れて、煮詰める。溶けても混ぜない。焦げたてきたら混ぜて、さっきと同量の水を入れる。シロップがはねたら機敏によける」

最近また風邪気味で、今日、熱を計ってみたら37度7分でした。
7が二つだからラッキーだわ! なんて自分に言い聞かせてみてもうまくいくわけがありません。
けっこう頻繁に風邪をひくので
「もしかしたら風邪をひいているときが普通で風邪をひいていないときがおかしいのかしら? じゃあ、風邪をひいてもしんどさを感じる必要はないわ」
なんて思おうにも鼻水じゅるじゅるでしんどさを実感、そんな11月下旬でございます。
でも、前向きに、「せっかく風邪をひいたのだから風邪を使ってblogの記事を書こう」なんて思いました。
37度7分って、微熱でしょうか? 少なくとも高熱ではないですよね。
大辞泉によると微熱とは平熱より僅かに高い熱だそうです。
高熱とは非常に高い温度だそうです。
僅かとか非常にとか曖昧でよくわからない!
で、今度はWikipediaで発熱について調べてみました。
Wikipediaによると
「微熱 ~37度5分
中程度の発熱 37度5分~38度5分
高熱 38度5分~」
だそうです。
ということはわたしは会った人に「どれぐらい熱があるの?」って尋ねられたら、「うーんとね、中程度の発熱なの」って答えればよいわけです。
きっと誰もそれが何度何分かって想像つかないでしょうけれど。
Wikipediaはこのblogでさも誰もが知っているかのように頻繁に取り上げていますが、実際、どの程度の知名度なのでしょう。「うーんとね、中程度の知名度なの」ってぐらいかしら?
Wikipediaとは読者が作るネット上の百科事典で、かなり多種多様な情報が詰め込まれています。
各言語毎にある、世界規模の百科事典です。日本語版では「BLANKEY JET CITY」から「ココナッツ娘。」まで、幅広く掲載されています(わかりづらい例えですいません。現在、289847本の記事があるそうです)。
その情報の信憑性はかなり高いと言われていて、2005年の12月にはNature誌が「WikipediaとBritannicaが同レベルの正確さを持っている」みたいな記事を書いていましたね(Britannicaとは世界的に有名な百科事典です)。
まあ、その記事には賛否両論あるようですが、実際、かなり高レベルな情報が掲載されていることは事実だと思います。
でも、この間、ちょっと気になることがありました。
以前もこのblogで紹介した、わたしが日本一のギャグ漫画家と思う「うすた京介」さんの公式個人サイト「めくるめけ日々」で自身についてのWikipediaの内容が間違っているということが記述されていたのです。
別にそのことでWikipediaに対するわたしの気持ちが変わるわけではないのですが、情報が氾濫するこの現代において、正しい情報ってその何割、あるいは何分何厘何毛ぐらいなのだろうと思ったのでございます。
皆様、情報の取り扱いには充分に注意いたしましょう!
おやすみなさいませ。
うすた京介 公式個人サイト めくるめけ日々
Wikipedia うすた京介
ピューと吹く!ジャガー 公式ページ
Wikipedia ブリタニカ百科事典
CNET Japan 「Wikipediaの情報はブリタニカと同じくらい正確」--Nature誌が調査結果を公表
ITmediaNews 「Wikipediaはブリタニカ並みに正確」記事に反論
Wikipedia 発熱
Wikipedia BLANKEY JET CITY
Wikipedia ココナッツ娘。
つい先日読んだ週刊誌に、数字の裏まで読む賢い人間になれということが書かれていました。
世の中には数字で表せないことがたくさんあります。
でも、数字で表さないとどうにもならないこともたくさんあると思います。
数字を上辺だけでとらえることはきっと危険でしょう。
でも、そこから、その数字が算出されるにいたった背景や精神状況なんかまで読み解くと、多くを知ることができる気がします。
物事を数字にすることで救われることがあれば、数字にすることで傷つくこともある……。
数字の話ばかりしているけれど、数字だけが大切だというつもりはないです。
数字ではないことも大切です。
どちらも大切だからこそ、わたしはちょっと嫌われがちな数字の味方をしている……のかしら?
ということで、掛け算シリーズ第三弾、ネット上にて発見した高速掛け算メソッド「繰り上がり分離法」のお話です。
たいていの人は九九と足し算はマスターしているということに着目した方法です。
わたしはこれを知ったとき、目からうろこの感動ものでした。
いつものごとく、152×231を計算しながら説明いたします。
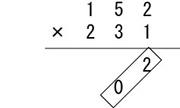
まず、普通の筆算と同じく、下一桁同士を掛けます。
ただ、普通と違うのは十の位と一の位を、斜めに書くことです。
ここでは2×1=02なので、1の左下に0を書きます。
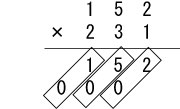
同じ要領で5×1と1×1の答えも書きます。
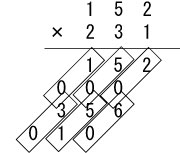
さらに続けて、152の十の位である5と231の各桁との掛け算の答えも書いていきます。
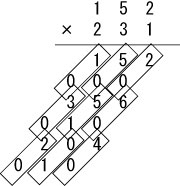
同じく152の百の位である1と231の各桁との掛け算の答えも書いていきます。
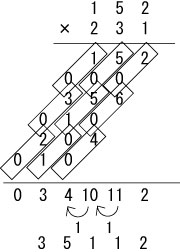
最後に計算結果を足し算して答えが出ます。
35112、正解です!
通常の筆算での桁上がりの処理を気にするのが最後の足し算だけのため、原理的には計算ミスがかなり減るものと思います。
実際には慣れの問題がありますが。
三回に亘った掛け算シリーズはこれで完結です。
誰でも知っている掛け算についての話題、シンプルだからこそ面白いとわたしは思いました。
この記事で身近なものへの好奇心が少しでも喚起され、さらにそれがクリエイティブ魂に繋がったら嬉しいわ! なんて思いました。
好奇心って、勇気や自己啓発以上の力を持つことがきっとけっこうあると思うのです。
数字が好きな人にはロマンチストが多いらしい。
それって、なんだか納得できます。
数字って、具体的な分、夢を見やすいと思うのです。
たとえば、スポーツで、現在100m走の世界記録はアサファ・パウエル選手の9秒77ですが、「9秒7を最初に切るのは世界の誰だろう」という夢を見られます。
走り幅跳びで世界記録はマイク・パウエル選手の8m95cmですが「人類初の9mジャンパーはいつ現れるだろう」と夢が見られます。
ということで(どういうことで?)、一昨日の「線を引くだけで掛け算」に続いてまた、ネット上で見つけた掛け算の手法です。
今回は前回のより実用性が高いと思います。
例として152×231を計算してみました。

まず、3桁×3桁なので、3×3の升目を書きます。
そして、左上から右下に向かって、「1」「5」「2」「2」「3」「1」の順番に記述します。
また、升目のすべての点を通るように、右上から左下への真っ直ぐな線を引きます。

次に、各升目に、欄外上部の数値と欄外右部の数値を掛け合わせた値を記述します。
値の十の位を左、一の位を右に書きます。
たとえば、左上の升目は「1×2=2」なので、「0」「2」と書いています。
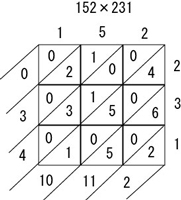
次に、升目内の値を、斜めにすべて足していきます。
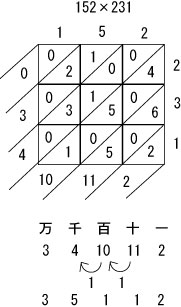
求めた数値(左と下の欄外に書かれた数字)を、左上から順番に並べます。
「3」「4」「10」「11」「2」です。
10以上のものは桁上がりさせます。
「3」「5」「1」「1」「2」になります。
152×231=35112で、正しい結果が求められました。
やはりやっていることは筆算と変わりませんが、計算ミスは減りそうに思います。
しっかりとした筆算を覚えるのがベストであるとしても、一時的に正しく計算したいときには良い方法ではと思います。
それに、こういうユニークな方法を知って、一般に敬遠されがちな「計算」という分野に対して興味を持ってもらえたら嬉しいです。
ちなみにこの掛け算話、まだ続きます。
次が完結編の予定です。
数字が好きです。
偏差値だったりなにもかもを数字化する風潮って否定的意見も多いようですが、わたしは肯定派です、多分。
わかりやすくなっているからこそ目標として明確だし、曖昧よりはずっと良いのではないかと。
数値化することで自分になにが足りないか、なにが足りているか、自分がどの位置にいるのかがわかります。
就職活動の能力についても偏差値かしようという動きがあるらしいですね。少し前にニュースで見ました。
ただ、もちろん、中途半端に一部分だけを数値化して、それですべてをわかった気になってしまう風潮もあるわけで、数字って簡単に人を欺けるわけで、そういう意味では反対派かもしれないです。
安易な数値化は反対ということかしら?
まあ、そんな話は置いておきまして、わたしはとにかく数字が好きです。
今日、ネット上で、ある掛け算の方法を知りました。
役に立つかどうかは別として、個人的にすっごい面白い計算方法だと思ったので紹介いたします!
以下、例題に画像をつけて説明いたします。
152×231を計算してみました。

まず、左上から順番に右上へと1本、5本、2本の真っ直ぐな線を引きます。
本数は計算する数値に合わせます。
今回は152だからこの本数です。

次に、231についても同じように、左下から順番に右下へと2本、3本、1本と真っ直ぐな線を引きます。
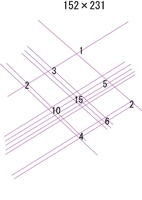
次に、各まとまりについて、交差点の数を数えます。
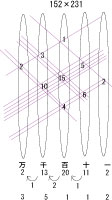
次に、左右の位置が同じ部分について、さきほど数えた交差点数を足し算します。
そして、右から順番に、一の位、十の位、百の位、千の位、万の位と考えます。
各桁10以上は桁上がりさせます。
答えが出ました!
35112、正解ですよね。
実際のところ、考え方は普通の筆算と変わらないですし、線を引く手間や交差点を数える手間があります。
ただ、数字が苦手だとこの方がわかりやすいと思いますし(数字を得意になることが本来の道だとしても、一時的な計算としては有益な方法かなと思います)、なにより、見た目的に面白いので気に入りました!
これとは違う面白い別の掛け算の方法も見つけましたので、後日紹介いたします!

「原産地はカザフスタン南部、キルギスタン、タジキスタン、中国の新疆ウイグル自治区など中央アジアの山岳地帯、コーカサスから西アジアにかけての寒冷地だといわれている。現在日本で栽培されているものは、明治時代以降に導入されたもの。 病害抵抗性、食味、収量などの点から品種改良が加えられ、現在7500以上の品種が栽培されている。亜寒帯、亜熱帯及び温帯で栽培可能だが、暑さに弱いため熱帯での栽培は難しい。
リンゴの花リンゴの木は落葉高木で4月 - 5月ごろに白い5弁花が開花する。リンゴの果実は直径約3 - 15センチメートル、重さ約35 - 1000グラムで、赤や緑色。
ポリフェノールの働きで、リンゴを食べることは人間にとっては抗酸化作用などにより老化を抑制する働きがあるといわれている。」
以上、Wikipediaより抜粋でございます。
幼少時代、The Beatlesのメンバーの名前にRingo Starrを見たとき「なぜ日本人ではないのにりんご?」と思いませんでしたか?
って、まあそのようなことはどうでもよいのでございます。
りんごって、他の果物と比べてなんだか特別視されているような気がするのはわたしだけでしょうか?
ニュートンの逸話や聖書など(聖書はイチジクという説もあるようですが)に登場するからなのかどうか、理由はともかく、他の果物に比べて格上の気がしてしまうのです。なんだか、神聖な感じがするというか……。
そんな位置づけを抱いているのはマッキントッシュマシンの愛好家とわたしだけかもしれないですが。
椎名林檎はいても椎名メロンや椎名スイカ、椎名ドリアンはいないわけですよ。
昨日、とある都内駅前で自転車を漕いでいたら、若い女性がりんごを丸かじりしながら歩いていたんです。
なんだか「かっこいいな」って思いました。魅力的でした。
りんごの丸かじりって、憧れませんか?
人通りの多い道で平然とりんごをかじっている姿は、潔く己の道を突き進んでいるような雰囲気であり、妙に惹きつけられたのです。
そして今朝、今度は道を歩きながらおにぎりをかじっている若い女性を見ました。
それはそれで潔いのですが、やっぱりりんごの丸かじりには勝てません。
わたし、大人になってから大根の丸かじりはしたことがあるけれど、りんごの丸かじりはしていないです……。
ちなみにわたしが好きな果物は柿と梨とみかんです。

ずっと前から話題は聞いていました、ラレコ先生によるFlashアニメのやわらか戦車を今日初めて見ました。
偶然訪れた方のblogからリンクがされていたもので。
流行に乗るのがいつも遅いのがわたしの売りです。
正直、アニメとしてものすごくレベルが高いかは判断できないです(Flashアニメの中では群を抜いて高いとは思います)。
ただ、歌がかなり気に入りました。この歌も作者さん自身が作られているのですよね、多分。
アニメと歌、その二つの要素が高い次元で組み合わさったことでこれだけの人気が出たのかなと勝手に分析しています。
歌の力ってやっぱりすごいなと思います。
心を惹きつけたりまとめ上げたり、人と人の間を光速で伝達する……。
ところで、このやわらか戦車の歌でエキセントリック少年ボウイの歌を思い出したのってわたしだけでしょうか?
♪以下、「エキセントリック少年ボウイ」のテーマより抜粋♪
がんばれ地球 がんばれ地球
ぼくは限界だ
くらわせろ くらわせろ
俺も知らない謎の小袋 80袋